分数基本性质视频,视频解析与核心要点概述

亲爱的读者们，你是否曾在某个夜晚，对着电脑屏幕，为了一道数学题而绞尽脑汁？分数，这个看似简单却又充满魔力的数学符号，今天就要来和你聊聊它的那些基本性质。让我们一起走进分数的世界，看看这个看似平凡的符号背后，隐藏着怎样的奥秘吧！

分数的起源：历史的足迹

分数的起源可以追溯到古埃及和巴比伦时期。那时的数学家们，为了解决实际问题，开始探索如何表示部分与整体的关系。而分数，就是这种探索的产物。随着时间的推移，分数逐渐发展成为一种独特的数学表达方式。

分数的基本性质：揭开神秘的面纱

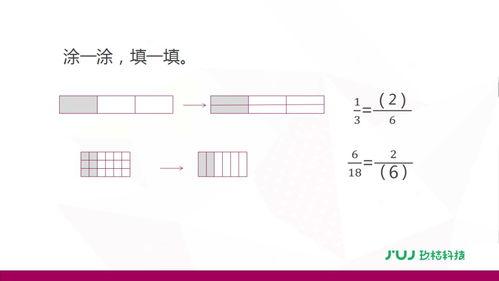
1. 分数的分子和分母

分数由分子和分母组成。分子位于分数线上方，表示被分割的部分；分母位于分数线下方，表示整体被分割成的等份数。例如，分数$\\frac{3}{4}$表示将一个整体分成4份，取其中的3份。

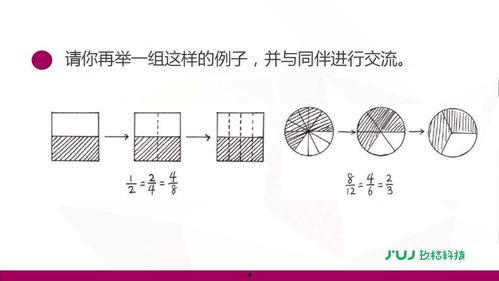
2. 分数的相等

两个分数相等，意味着它们表示的是同一个数值。例如，$\\frac{1}{2}$和$\\frac{2}{4}$是相等的，因为它们都表示将一个整体分成2份，取其中的1份。

3. 分数的加减乘除

分数的加减乘除遵循一定的规则。加法和减法时，分母必须相同；乘法时，分子与分子相乘，分母与分母相乘；除法时，分子与分母分别相除。

4. 分数的倒数

分数的倒数是指分子和分母互换位置后得到的分数。例如，$\\frac{3}{4}$的倒数是$\\frac{4}{3}$。

5. 分数的约分

约分是指将分数的分子和分母同时除以它们的最大公约数，使分数变得更加简洁。例如，$\\frac{6}{8}$可以约分为$\\frac{3}{4}$。

分数的应用：生活中的魔法

分数在我们的生活中无处不在。以下是一些常见的分数应用场景：

1. 烹饪

烹饪时，我们经常需要按照一定的比例添加各种食材。例如，制作蛋糕时，需要按照$\\frac{1}{2}$的量加入面粉、$\\frac{1}{3}$的量加入糖等。

2. 购物

购物时，我们常常会遇到打折、优惠等活动。这时，我们需要计算折扣后的价格，也就是原价与折扣率的乘积。

3. 建筑设计

建筑师在设计建筑时，需要考虑各种比例关系。例如，门窗的大小、楼层的高度等，都需要按照一定的比例进行设计。

分数的拓展：探索未知的领域

分数的奥秘远不止于此。在数学的各个分支中，分数都有着广泛的应用。以下是一些与分数相关的拓展领域：

1. 概率论

概率论是研究随机事件发生可能性的数学分支。在概率论中，分数被用来表示事件发生的概率。

2. 复数

复数是由实数和虚数构成的数。在复数中，分数被用来表示虚数单位$i$。

3. 微积分

微积分是研究函数变化规律的数学分支。在微积分中，分数被用来表示导数和积分。

亲爱的读者们，分数的世界充满了神奇和奥秘。通过本文的介绍，相信你已经对分数有了更深入的了解。让我们一起继续探索这个充满魅力的数学世界吧！